现代化工过程通常都装有大量的测量传感器，如温度、流量和压力传感器等。一些测量传感器会用于闭环控制，而另外一些传感器只用于过程监测。在正常条件下，大多数传感器得到的测量值是高度相关的。因此，这*为传感器的故障诊断提供了宝贵的解析冗余。这些测量值的相关性主要源于支配过程运行的物理与化学原理，如：质量与能量平衡等。

传感器异常检测
       单变量和多变量的统计过程控制技术可用于检测如下的传感器异常：
           (1)异常测量值 这种情况主要是由于传感器的故障引起的。

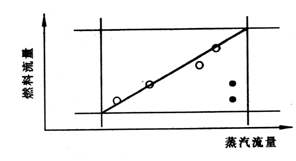
           (2)多个传感器偏离正常的相关条件

            在正常条件下，过程的测量值通常表现出较强的相关性。这些测量相关性为我们提供了必要的冗余，可用于故障传感器的检测、辨识与重构。这可以通过比较过程的测量值与基于标称模型的估计值之间的差别来实现。

            可以采用统计方法来建立过程的标称模型，如；主元分析方法(principle component analysis—PCA)以及部分*小二乘(partial least squares—PLS)算法等。

           (3)被监测过程的瞬态变动

            所不期望的测量瞬态变动，例如：振荡、或者在批处理过程中的不寻常的趋向性，一般是由于非正常的操作条件引起的。

            检测这类异常通常采用的是动态统计模型，或卡尔曼滤波器。出于安全方面的原因，大多数化工过程的反应都比较缓慢。这类瞬态变动可以看成是伪稳态。因而可近似采用稳态的相关分析方法来进行处理。采用一些滤波技术也可以进一步减弱瞬态变动的影响。

            采用主元分析进行过程监测与故障检测是近年来才发展起来的。由于数据的相关性，一些主要的分量*可以充分描述全部数据的方差。基于主元分析可以区分如下(4)和(5)两类异常条件。

           (4)传感器相关故障

            在这种情况下，PCA模型被破坏增加。残余向量的欧氏范数将显著增加。

           (5)变动过大

            用于描述操作变化的变量超过了正常的范围。

传感器故障
       某一故障传感器通常会破坏与其他传感器的正常的相关性。当异常条件被检测到以后，此特性可用于故障传感器的辨识。

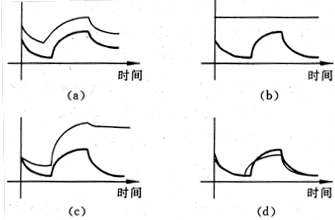
       只考虑四种类型的传感器故障，即：偏差、彻底失效、漂移、精度下降。图2．2给出了这四种故障的示意图。